
이 문제는 어떤 포인트에 맞춰 이분 탐색을 할 지 정하기가 어려운 문제였다. 많은분들이 풀이해놓으신 내용을 보고 어떤 부분들에 중점을 두고, 어떤 방식으로 조금이라도 더 시간을 줄여야할 지 알 수 있었기 때문에 정리해보고자 한다.
✍️ 우선, 이 문제에서 이분 탐색을 사용해야하는 포인트를 먼저 알아보자.
B[k]를 구함에 있어서, B[k]는 흔히 배열 B의 K번째 요소로 해석된다. 하지만 이를 방향을 돌려서 생각해보면 해당 요소는 자신 앞에 'K - 1'개의 요소가 있다는 의미가 된다. 더 나아가서, 이 배열이 오름차순으로 정렬된 배열이라는 전제 하에는 어떨까? 이는 곧 자기 자신과 같거나(자기 자신을 포함) 자신보다 작은 요소가 K개 있다는 의미가 된다. 즉, 이분탐색은 여기서 사용되야 한다. 특정 요소의 값을 이분탐색의 검증값(mid)로 두면서 이 값보다 작거나 같은 요소가 몇 개 있는지(cnt) 확인한 후, 이 값이 K보다 크거나 같아야 한다.
while(lt <= rt) {
int mid = (lt + rt) / 2;
int cnt = 0;
// mid보다 작은 원소의 개수 구하기(cnt 증가)
// ...
if (cnt >= K) rt = mid;
else lt = mid + 1;
}
✍️ 그렇다면 다음으로는 mid값이 변함에 따라 이 값보다 작은 원소의 개수를 어떻게 구하면 될까? 배열 A의 원소들로 이루어진 배열 B를 정렬했다고 가정해보자. 가장 쉬운 방법은 for문을 돌려 mid값이 나올 때까지 개수(cnt)를 증가시키는 방법일 것이다. 하지만 이 문제의 입력 조건을 보면, N은 105 보다 작거나 같은 자연수이다. 즉, 최대값이 입력될 경우에는 배열 B의 원소의 개수는 N*N의 값인 10,000,000,000 이 될 수도 있는 것이다. 이렇게 될 경우에는 지나치게 많이 루프를 돌아야 하는 상황이 발생하므로 다른 방법을 찾아보자.
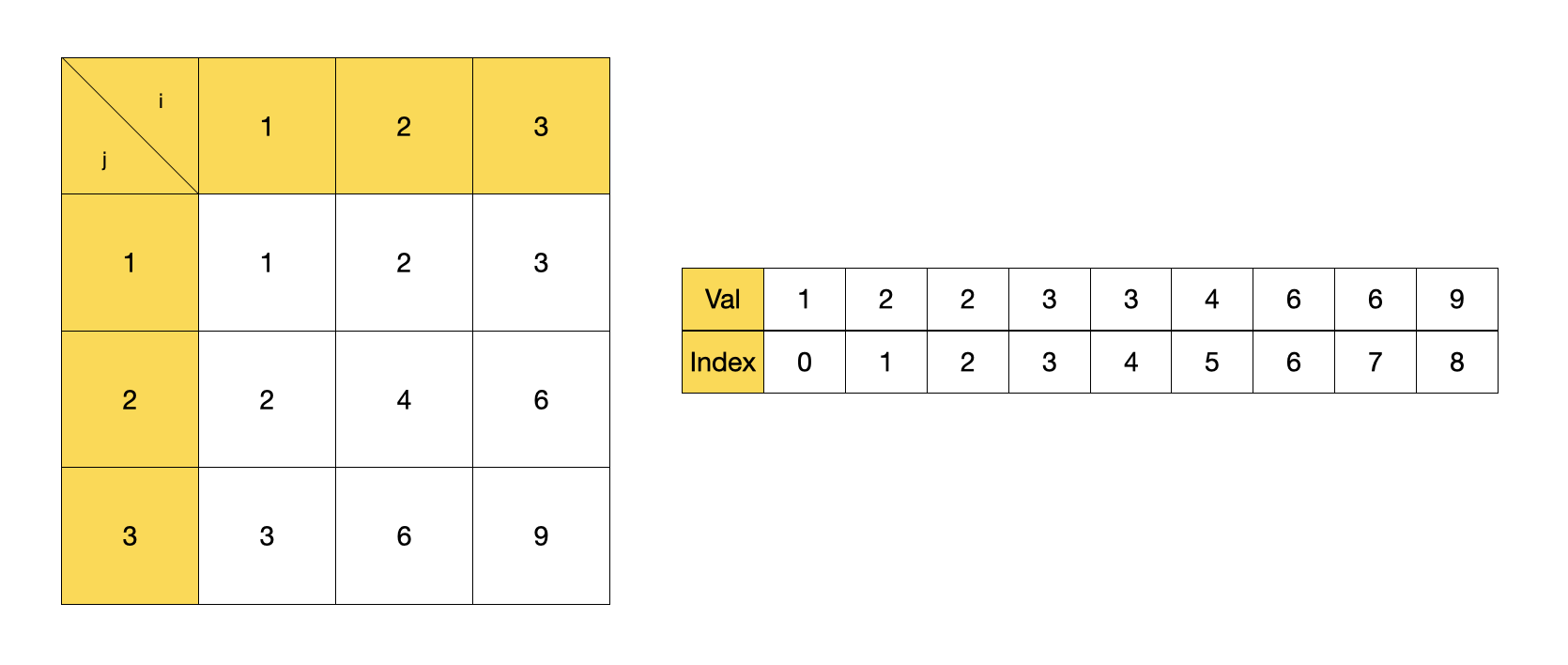
✍️ a가 b보다 작다. 라는 의미는, b를 a로 나누었을 때 위의 좌측 이미지를 통해서 배열의 행들의 원소값들을 눈여겨 보자. 만약 검증값(mid)이 4일 경우, A[1]에서는 [1, 2, 3], A[2]에서는 [2, 4], A[3]에서는 [3]이 4보다 작은 수가 된다. 특징을 살펴보면, 검증값보다 작은 원소들의 수는 검증값을 해당 행의 인덱스로 나눈 결과의 몫과 일치한다. 하지만 유의해야 하는 점이 있다. 만약 N = 3, K = 8이라면 첫 번째 행에서 B[K]보다 작은 원소의 수는 8을 1로 나눈 몫인 8일까? 아니다. 해당 배열은 한 행에 3개의 원소를 가지므로 이 때에는 3이 맞다. 따라서, 코드 상으로 Math.min 메서드를 이용해 나눈 몫이 N보다 클 때는 N을 반환하게 해주어야 한다.
while(lt <= rt) {
int mid = (lt + rt) / 2;
int cnt = 0;
for (int i = 0; i < N; i++) cnt += Math.min(mid / i, N);
if (cnt >= K) rt = mid;
else lt = mid + 1;
}
✍️ 그러면 우선 탐색 범위를 정의하기 위해 lt와 rt값을 정의하자. 모든 원소 값은 행 x 열의 값이고, 행과 열의 인덱스는 1부터 시작하기 때문에 가장 작은 원소는 1일 것이다. 그러므로 lt는 1이 되면 된다. 그럼 rt는 어떨까? 배열의 가장 큰 원소라고 생각하면 편하다. 그렇게 되면 N*N이 될 것이다. 여기서 더 줄일 수 있는 방법이 있다. 우선, 우리가 찾고자 하는 특정 원소 값(B[K])의 범위는 1 ≤ B[K] ≤ N*N이 된다. K값은 어떨까? K는 1 ~ N*N의 범위 내에 존재해야 하며, 당연히도 가장 클 때가 마지막 인덱스인 N*N이다. 따라서 정리해보자면 B[K]의 범위는 1 ≤ B[K] ≤ K가 된다.
int lt = 1, rt = K;
while(lt <= rt) {
int mid = (lt + rt) / 2;
int cnt = 0;
for (int i = 0; i < N; i++) cnt += Math.min(mid / i, N);
if (cnt >= K) rt = mid;
else lt = mid + 1;
}
✍️ 마지막으로, 반환해줘야 하는 값은 무엇인가? while문이 끝나면서 찾고자 하는 값 또는 그 이상의 값이 시작되는 지점인 LowerBound를 출력해주면 된다. 그러면 아래와 같이 코드는 완성된다. 🙌
int lt = 1, rt = K;
while(lt <= rt) {
int mid = (lt + rt) / 2;
int cnt = 0;
for (int i = 0; i < N; i++) cnt += Math.min(mid / i, N);
if (cnt >= K) rt = mid;
else lt = mid + 1;
}
return lt;
cf. 여기서, 왜 K보다 크거나 같은 값을 확인하느냐? 라고 한다면 예시를 들어보겠다. 문제에서 제공하는 예시 답안을 참고하여 N(3), K(7)이 주어졌을 때의 경우를 보자. 배열 A의 행(i)과 열(j)이 1부터 시작해 N(3)까지 존재한다면 아래와 같은 요소들이 존재할 것이다. 이를 배열 B에 넣을 경우, 배열 B는 [1, 2, 2, 3, 3, 4, 6, 6, 9]의 형태를 가지게 된다. 이 때 B[7]은 6이다. 실제로 mid값이 6이라고 여기고 앞의 요소들의 개수를 세어보면 7, 8(6은 2개 이므로)임을 알 수 있다. 반대로, mid값이 그 직전 요소인 4라고 여겨보자. 앞의 요소들은 6개이다. 만약 배열의 원소들을 모두 정렬시켜 mid값이 변경될 때마다 앞의 원소를 세는 루프문을 돌리는 경우에는 정확한 인덱스를 알 수 있을 것이다. 하지만 위와 같은 방식으로 구할 때에는 중복되는 수일 경우에는 자신의 앞 원소를 세어도 정확하게 K와 일치하지 않을 수도 있다. 이 때는 자신과 같거나 큰 수가 K보다 작아서는 안되는 값 중에 최솟값을 구할 수 밖에 없다. 이분탐색의 형식상 LowerBound, UpperBound값을 찾기까지 계속해서 탐색 범위의 양 끝 인덱스를 변경시키는데 이 때 검증값(mid)은 원소로 있는 값일 수도 있지만, 아닌 값일 수도 있다. 만약 mid값이 5라면, 4일 때와 마찬가지로 6이 나올 것이다.
작성 코드
public class Main {
private int solution(int n, int k) {
int lt = 1, rt = K;
while(lt <= rt) {
int mid = (lt + rt) / 2;
int cnt = 0;
for (int i = 0; i < N; i++) cnt += Math.min(mid / i, N);
if (cnt >= K) rt = mid;
else lt = mid + 1;
}
return lt;
}
public static void main(String[] args) {
Main main = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
System.out.println(main.solution(n, k));
}
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| 알고리즘) 배열의 모든 부분집합 구하기(DFS) (0) | 2022.07.27 |
|---|---|
| 알고리즘) 재귀 함수와 메모이제이션(Memoization)으로 피보나치 수열 구하기 (0) | 2022.07.26 |
| 알고리즘) 숫자 카드 2(백준 이분탐색 10816번) (0) | 2022.07.17 |
| 알고리즘) 랜선 자르기(백준 이분탐색 1654번) (0) | 2022.07.17 |
| 알고리즘) 나무 자르기(백준 이분탐색 2805번) (0) | 2022.07.17 |
