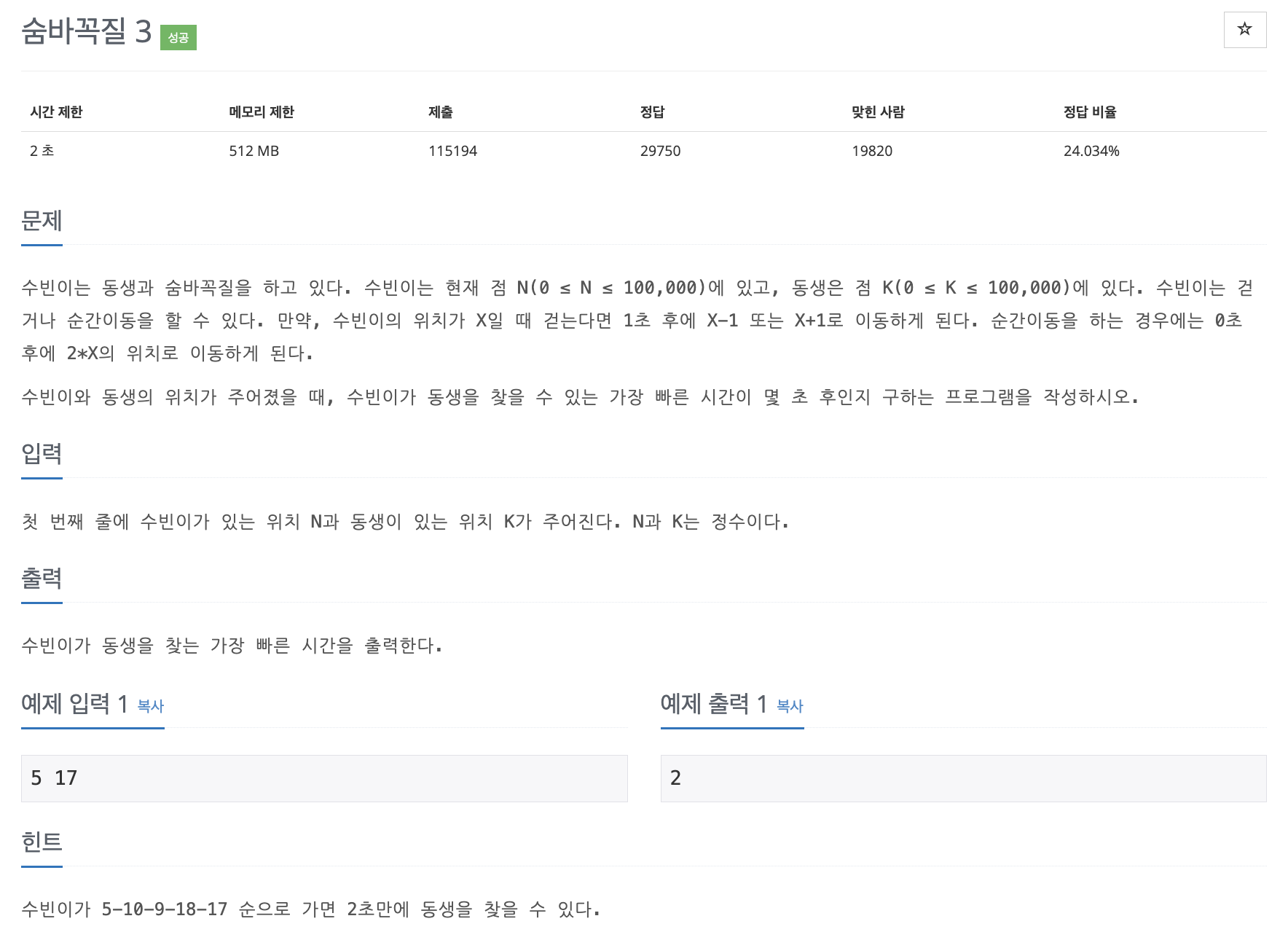
문제
풀이
특정 노드 간의 최단 거리를 구하는 문제로 BFS로 풀 수 있긴 하지만, 간선의 값이 일정하지 않기 때문에 (0일 수 있기 때문) 0-1 BFS 방식으로 풀 수도 있고 다익스트라 알고리즘으로 풀 수도 있다.
0-1 BFS로 풀 경우, 일반적으로 그래프 문제에서 BFS를 이용해 최단거리를 구하는 경우에는 항상 간선이 1이라는 전제가 깔린 문제가 많아 목적지값이 poll될 때, 큐를 더이상 돌리지 않아도 된다. 하지만 이 문제에서는 간선 값이 0인 경우가 존재하므로, 모든 값이 큐에 들어갔다 나와야 한다. (이 부분을 놓쳐서 여러 번 틀렸다..)
이는, 현재 위치가 `X`라고 하고 `X * 2`만큼 이동할 때에는 시간(이동에 소요되는 비용)이 증가하지 않기 때문에 더 나중에 찾아진 경우에도 이미 찾아진 값(시간)보다 더 작을 수 있기 때문이다.
또한, `X * 2`를 `X + 1`이나 `X - 1` 보다 먼저 실행함으로써 더 적은 비용이 드는 경우가 먼저 찾아질 가능성을 높여 메모리나 시간을 아낄 수 있을 것으로 여겨진다.

BFS 사용
import java.util.*;
// BFS 방식
public class Main {
private boolean[] visited = new boolean[100001];
int bfs(int node, int end) {
Queue<Node> q = new LinkedList<>();
q.offer(new Node(node, 0));
int answer = Integer.MAX_VALUE;
while (!q.isEmpty()) {
Node n = q.poll();
visited[n.key] = true;
if (n.key == end) {
answer = Math.min(answer, n.cost);
}
if (n.key * 2 <= 100000 && !visited[n.key * 2]) {
q.offer(new Node(n.key * 2, n.cost));
}
if (n.key + 1 <= 100000 && !visited[n.key + 1]) {
q.offer(new Node(n.key + 1, n.cost + 1));
}
if (n.key - 1 >= 0 && !visited[n.key - 1]) {
q.offer(new Node(n.key - 1, n.cost + 1));
}
}
return answer;
}
public void solution() {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
int result = bfs(a, b);
System.out.println(result);
}
public static void main(String[] args) {
Main main = new Main();
main.solution();
}
private static class Node {
int key;
int cost;
public Node(int key, int cost) {
this.key = key;
this.cost = cost;
}
}
}
다익스트라
import java.util.*;
public class Main {
private int MAX_VALUE = 100_000; // 0 <= a <= 100_000, 0 <= b <= 100_000
private int INF = 100_000; // a와 b가 각각 0과 100,000일 경우 최대 거리는 100,000
public void solution() {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
// 각 인덱스를 키로 갖는 노드들에 도달하는데 걸린 최소 시간
int[] distance = new int[MAX_VALUE + 1];
Arrays.fill(distance, INF);
// 방문한 노드와 그렇지 않은 노드 구분
boolean[] visited = new boolean[100001];
// 현재 위치(a에서 시작해 이동)에서 갈 수 있는 노드들로의 거리 계산 후 큐에 저장
// -> 다음으로 이동할 위치는 가장 우선순위가 높은 비용의(여기서는 최소힙이라 가장 비용이 적은) 노드
PriorityQueue<Node> q = new PriorityQueue<>((n1, n2) -> n1.cost - n2.cost);
q.offer(new Node(a, 0));
distance[a] = 0;
while (!q.isEmpty()) {
Node node = q.poll();
visited[node.key] = true;
int pos;
pos = node.key + 1;
if (isValid(pos) && !visited[pos] && distance[pos] > node.cost + 1) {
distance[pos] = node.cost + 1;
q.offer(new Node(pos, distance[pos]));
}
pos = node.key - 1;
if (isValid(pos) && !visited[pos] && distance[pos] > node.cost + 1) { // node.cost > node.cost + 1 일 가능성은 없으니 생략
distance[pos] = node.cost + 1;
q.offer(new Node(pos, distance[pos]));
}
pos = node.key * 2;
if (isValid(pos) && !visited[pos] && distance[pos] > node.cost) {
distance[pos] = node.cost;
q.offer(new Node(pos, distance[pos]));
}
}
System.out.println(distance[b]);
}
private boolean isValid(int value) {
return 0 <= value && value <= 100_000;
}
public static void main(String[] args) {
Main self = new Main();
self.solution();
}
private static class Node {
int key;
int cost;
public Node(int key, int cost) {
this.key = key;
this.cost = cost;
}
}
}`visited`를 이용해 방문한 노드를 구분하여 방문하지 않은 노드만 방문하게 구현을 했는데, 방문한 노드를 구분하지 않아도 정답이 나온다.
Cf. 다익스트라 알고리즘
다익스트라 알고리즘은 그리디 알고리즘과 동적 계획법(DP, Dynamic Programming)을 기반으로 한다.
그리디 알고리즘
그리디(Greedy) 알고리즘이란 순간 순간에 최선의 선택을 하는 알고리즘으로, 최종 결과가 최선의 결과라는 보장은 없다.
그리디 알고리즘 기반의 알고리즘 및 자료구조
1. 우선순위 큐(기본적으로 최소힙 형태로 구성된다.)
우선순위가 높은 값을 먼저 꺼내어 각 순간에 최선의 선택을 한다.
// 만약 최대힙 형태로 구성하고 싶다면 PriorityQueue 생성자의 인자로 Collections.reverseOrder() 전달
PriorityQueue<T> queue = new PriorityQueue<>(Collections.reverseOrder());
2. 다익스트라 알고리즘
최단 경로 탐색 알고리즘이다. 특히나 그래프의 최단거리 문제지만 간선의 가중치가 다른 경우에도 다익스트라 알고리즘으로 해결할 수 있다. (가중치가 0과 1 뿐인 경우 0-1 BFS 방식으로도 해결할 수 있다.)
다익스트라 알고리즘 동작 방식
1. 출발 노드를 선택한다.
2. 각 노드에 도달하는 데 걸리는 최단 거리를 저장하기 위한 배열 d를 선언하고, 요소를 모두 INF로 채운다. (이 때, INF는 문제에서 추론할 수 있는 최대값을 넣어도 되고, Integer.MAX_VALUE를 넣어도 된다.)
3. 출발 노드를 방문한다. 이 때 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
4. 방문하지 않은 노드 중 가장 비용이 적은 노드를 선택(이를 위해 `visited` 배열을 두어 방문한 곳인지를 확인하고, PriorityQueue를 이용해 큐에 들어있는 곳 중 비용이 가장 작은 값인 노드를 꺼내온다.)
5. 해당 노드를 방문해 연결된 다른 노드들로 갈 경우 드는 비용을 이용해 최소 비용을 갱신한다. (기존의 최소 비용 값이 있는 노드라 하더라도 이후에 도달하는데 드는 비용이 더 적은 경우가 발견되면 갱신한다.)
6. 4 ~ 5번 과정을 반복한다.
7. d[목적지] 값을 반환한다.
예제) 아래와 같은 그래프에서 다익스트라 알고리즘을 통해 A에서 F로 이동할 때 드는 최단 거리를 찾는 문제이다.

| 방문한 노드 (편의를 위해 삽입 순서대로 작성) |
이동거리 확인 | 각 노드에 도달하는데 든 비용 | 방문 안한 노드 |
| [] | A -> A | [0, INF, INF, INF, INF, INF] | [A, B, C, D, E, F] |
| [A] | A -> B, C, D | [0, 4, 3, 7, INF, INF] | [B, C, D, E, F] |
| [A, C] | C -> A, B, D, F | [0, 4, 3, 7, INF, 6] | [B, D, E, F] |
| [A, C, B] | B -> A, C, E, F | [0, 4, 3, 7, 7, 6] | [D, E, F] |
| [A, C, B, F] | F -> B, C | (변동 없음) | [D, E] |
| [A, C, B, F, D] | D -> A, C | (변동 없음) | [E] |
| [A, C, B, F, D, E] | E -> B | (변동 없음) | [] |
'자료구조 및 알고리즘' 카테고리의 다른 글
| 알고리즘) 프로그래머스 PCCE 기출문제 1회 10번(해시 사용) (0) | 2024.08.11 |
|---|---|
| 알고리즘) 더 맵게(프로그래머스, 힙 활용, Java) (0) | 2024.08.07 |
| 힙 정렬(Heap Sort) 구현하기(Java) (0) | 2024.08.07 |
| 배열(Array)을 이용한 힙(Heap) 구현 (0) | 2024.08.06 |
| 알고리즘) 네트워크(프로그래머스, BFS 활용, Java) (0) | 2024.08.03 |
