문제 ✨
조합수는 원래대로라면 \({n}\mathrm{C}{r} = n!/(n - r)!r!\) 로 계산합니다. 하지만 여러분은 이 공식을 쓰지않고 다음 공식을 사용하여 재귀를 이용해 조합수를 구해주는 프로그램을 작성하세요.
$${n}\mathrm{C}{r} = {n-1}\mathrm{C}{r-1} + {n-1}\mathrm{C}{r}$$
입력
첫째 줄에 자연수 $ n(3<=n<=33) $과 $ r(0<=r<=n) $이 입력됩니다.
출력
첫째 줄에 조합수를 출력합니다.
풀이 ✨
고등 수학의 확률과 통계와 관련된 내용으로, 위의 수식의 예시를 들면 아래와 같다. n이 5일 때 조합될 수 있는 원소들로 구성된 배열은 다음과 같다.
{1, 2, 3, 4, 5}이 때 위의 5개의 원소 중 3개의 요소를 선택하는 경우는 \({4}\mathrm{C}{2} + {4}\mathrm{C}{3}\)으로 표현할 수 있는데, \({4}\mathrm{C}{2}\)는 5가 들어가는 경우에 나머지 4개의 수 중 2개의 수를 선택하는 경우를 의미하고, \({4}\mathrm{C}{3}\)은 5가 들어가지 않는 경우에 나머지 4개의 수 중에서 3개의 수를 고르는 상황을 의미한다.
이를 재귀 함수로 만든다면 이러하다. \({n}\mathrm{C}{r}\)을 구함에 있어서, \({n}\)과 \({r}\)이 같아지면 그 값은 항상 1이 나오며, \({r}\)이 0이 되어도 그 값은 1이 된다. 트리의 최하단에는 항상 1이 존재한다. 여기서부터 계속해서 더해나가는 것이다.
static int n;
static int r;
static int[] result; // number of combination. (for memoization)
int[] getCombinations(int v, int x) {
if (x > 0 && v == x) {
arr[v] = getCombinations(v - 1, x - 1) + getCombinations(v - 1, x);
}
}\({5}\mathrm{C}{3}\)의 재귀 구조를 트리로 그려보면 다음과 같다. 항상 최하단 노드들은 \({r}\)이 0이 되거나 \(n == r\)이 되는 경우이다. 이 값들은 전부 1이므로 이 경우에만 그 값을 1로 두고, 상위 노드의 값을 구하기 위해서는 이 들을 상향식으로 더해가면 된다.
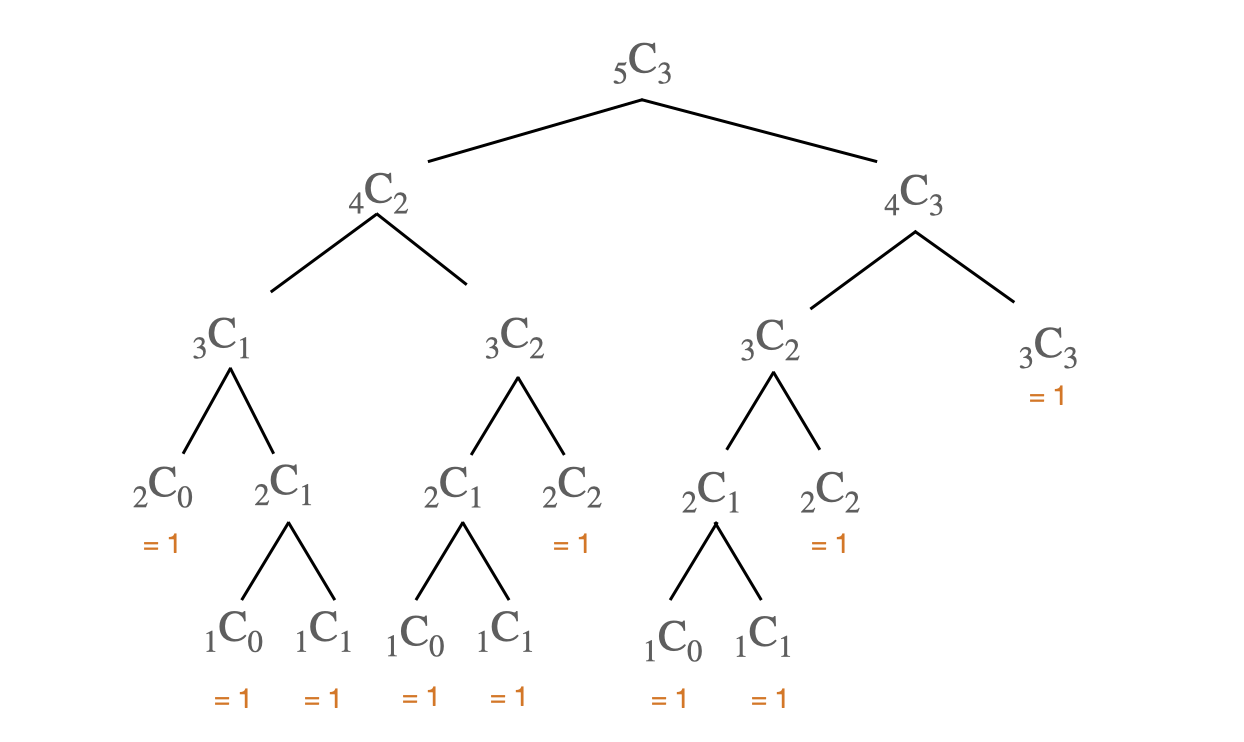
결론적으로 재귀 함수의 코드는 아래와 같이 된다.
static int n;
static int r;
static int[][] result;
int getCombinations(int v, int x) {
if (v == x || x == 0) {
result[v][x] = 1;
} else {
result[v][x] = getCombinations(v - 1, x - 1) + getCombinations(v - 1, x);
}
return result[v][x];
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| 알고리즘) 미로 탐색(DFS 활용) (0) | 2022.08.14 |
|---|---|
| 알고리즘) 수열 추측하기(트리 DFS 활용) (0) | 2022.08.14 |
| 알고리즘) 트리의 부모 찾기(백준 11725번) (0) | 2022.07.30 |
| 알고리즘) 트리 순회(백준 1991번) (0) | 2022.07.30 |
| 알고리즘) 송아지 찾기 1(BFS : 상태트리탐색) (0) | 2022.07.27 |
